Question C:
- The formula for the Z-score is given below:

- Thus, we can calculate the Z-score as follows:
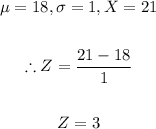
- The Z-score is 3
Question D:
- We need to calculate the Z-score of the height of 18.6ft and then convert the Z-score to probability using a Z-score calculator.
- The Z-score is calculated as follows:
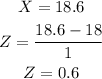
- The probability P(Z < 0.6) is depicted below:
- Thus, the probability of getting a giraffe shorter than 18.6ft is 0.72575
Question E:
- Again, we need to find the Z-scores for both 17.2ft and 18ft and then find the probability:
P(17.2 < Z < 18)
- The Z-scores are gotten as follows:
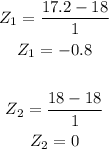
- Thus, the probability of obtaining heights corresponding to the above Z-scores is:
- Thus, the probability of getting a giraffe with a height between 17.2 and 18ft tall is 0.28814
Question F:
- The 80th percentile corresponds to 80/100 = 0.8 probability.
- We should find the corresponding Z-score before finding the value of X, using the Z-score formula
- The corresponding Z-score of 0.8 is 0.842
- The value of X is:
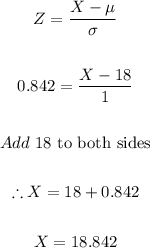
- The 80th percentile value is 18.842