The probability of a dry day is P(D)=1/8
If the day is dry, the probability of Blake cycling to work is P(C/D)=5/14
If the day is dry, the probability that Blake drives to work is P(V/D)=5/14
If the day is dry, the probability that Blake takes the train to work is P(T/D)=2/7
If the day is wet (W) the probability that Blake cycles to work is P(C/W)=3/16
If the day is wet (W) the probability that Blake drives to work is P(V/W)=1/4
If the day is wet (W) the probability that Blake takes the train to work is P(T/W)=9/16
Assuming that the events "The day is Wet" and "The day is dry" are complementary, we calculate the probability of W as:
P(W)=1-P(D)
P(W)=1-1/8
P(W)=7/8
You have to calculate the probability of Blake taking the train to work, regardless if the day is dry or wet, to do so you have to add the probability of him taking the train and the day being dry plus him taking the train and the day being wet, symbolucally:
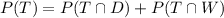
The given probabilities are conditional probabilities, considering the definition of the conditional probability, which states that:
Given two dependent events A and B, the probability of A given that B has appened is equal to the probability of A and B divided the probability of B, symbolically:
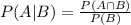
Using this definition we can determine the intersections of the events "Take the train to work" and "The day is dry":
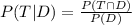
We know the conditional probability P(T|D) and the probability of th day beign Dry P(D), so we can calculate the intersection as:

Now calculate the probability of "Take the train to work" and "The day is wet":

We know P(T|W) and P(W), so we can calculate the intersection as:
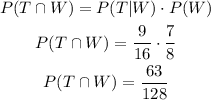
Finally calculate the probability of him taking the train
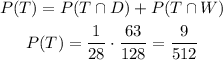
The probability that he takes the train to work is 9/512