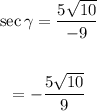Question

Suppose that is an angleand y is not in the first quadrant. Compute the exact value of secyYou do not have to rationalize the denominator. with * cot gamma = 9/13

Answer 1

The answer is :

`-(5√(10))/(9)`

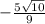
EXPLANATION :

Note that cotangent is only positive when the angle is in the first or third quadrant.

Since y is not in the first quadrant, it must be in the third quadrant.

So the x and y are both negative.

An angle with a terminal point (x, y)

The cotangent is x/y

We can equate :

`\cot\gamma=(9)/(13)=(x)/(y)`

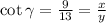
Since x and y are both negatives, x = -9 and y = -13

We can have the triangle :

The hypotenuse will be :

`\begin{gathered} c=√((-9)^2+(-13)^2) \\ c=5√(10) \end{gathered}`

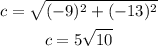
We are asked to find the value of sec y.

In an angle with a terminal point (x, y)

The secant is :

`\sec\gamma=\frac{\text{ hypotenuse}}{x}`

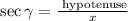
The hypotenuse is 5√10 and x = -9

The value of sec will be :

`\begin{gathered} \sec\gamma=(5√(10))/(-9) \\ \\ =-(5√(10))/(9) \end{gathered}`