Given:
We are to fit x number of cylindrical kegs in a truck.
Dimensions of the kegs: Diameter 9 inch, height 32 inch.
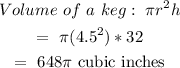
Volume of the truck: height * length* breadth
= 9*7*53
=3339 cubic ft
= 40068 inches
To find the amount of kegs that can fit, we divide the volume of the truck by the volume of the kegs and round off to a reasonable number.
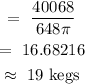
2.) To find the volume of space left-over:
Volume of 19 kegs:
