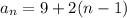Question

The sequences below are either arithmetic sequences or geometric sequences. For each sequence, determine whether it is arithmeticthor geometric, and write the formula for the nterm a, of that sequence.SequenceTypethnterm formula2 8 08

Answer 1

A geometric sequence is one where each term is the previous one by a constant term we call the common ratio. The quotient between consecutive numbers is the common ratio.

An arithmetic sequence is one where each term is at the same distance from the next. The difference between consecutive numbers is constant, we call that constant common difference.

The first sequence given is:

6, 12, 24

The first term, 6, is at a distance of 6 from the next term, 12. The term 12 is at a distance of 12 from the next one. Since the distance between two consecutive terms is not constant, the sequence is not arithmetic.

Let's see if its a geometric sequence:

`\begin{gathered} (12)/(6)=2 \\ . \\ (24)/(12)=2 \end{gathered}`

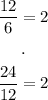
The quotient is constant, thus this is a geometric sequence.

The formula for the nth term of a geometric sequence is:

`a_n=a_1r^(n-1)`

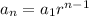
Where:

a_1 is the first term

r is the constant ratio

n is the term we want to find.

In this case:

a_1 = 6

r = 2

Thus, the nth term equation of this sequence is:

`a_n=6\cdot2^(n-1)`

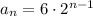
The second sequence is:

9, 11, 13...

We can see that the first term is at a distance of 2 from the second term. The second term is at a distance of 2 from the third term.

Since the distance between two consecutive terms is constant, This is an arithmetic sequence.

The formula for the nth term of an arithmetic sequence is:

`a_n=a_1+d(n-1)`

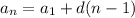
Where d is the common difference.

In this case:

a_1 = 9

d = 2

Thus, the nth term equation of this sequence is:

`a_n=9+2(n-1)`