Step-by-step explanation
We have the equation:
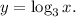
a) To express x in terms of y, we take into account the following property of logarithms:
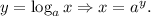
Choosing a = 3, we have:
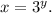
b) Now, we evaluate this function for the values y = -2, -1, 0, 1 and 2. To do that, we simply replace the value of y in the last equation, then we simplify the result:
1) y = -2
Replacing y = -2 in the equation of x, we have:
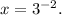
Now, the negative power of a number can be written as the positive power but in the denominator:
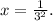
The 3 square is equal to 3*3 = 9, so we have:
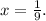
So the point for y = -2 is:
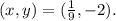
2) y = -1
![y=-1\operatorname{\Rightarrow}x=3^(-1)=(1)/(3^1)=(1)/(3)\Rightarrow(x,y)=((1)/(3),-1).]()
3) y = 0
![y=0\operatorname{\Rightarrow}x=3^0=1\Rightarrow(x,y)=(1,0).]()
4) y = 1
![y=1\operatorname{\Rightarrow}x=3^1=3\Rightarrow(x,y)=(3,1).]()
5) y = 2
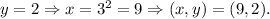
Answer
a) The exponential form is: x = 3^y
b) The values of x for the table are:
• y = -2 ⇒ (,1/9,, -2)
,
• y = -1 ⇒ (,1/3,, -1)
,
• y = 0 ⇒ (,1,, 0)
,
• y = 1 ⇒ (,3,, 1)
• y = 2 ⇒ (,9,, 2)