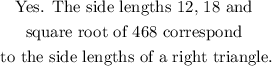Question

Will these side lengths form a right triangle? Square root of 468, 12 and 18

Answer 1

If three numbers are side lengths of a right triangle, then, from the Pythagorean Theorem, the square of the longest side must be equal to the sum of the squares of the smaller sides.

In this case, the square root of 468 is greater that 12 and 18. Then, if those were the side lengths of a right triangle, then:

`12^2+18^2=(\sqrt[]{468})^2`

Simplify each member of the equation to check if the equation is true or not:

`\begin{gathered} \Rightarrow144+324=468 \\ \Rightarrow468=468 \end{gathered}`

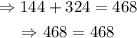
Since the equation is true, then the given numbers are indeed the side lengths of a right triangle.

Therefore, the answer is:

`\begin{gathered} \text{Yes. The side lengths 12, 18 and} \\ \text{square root of 468 correspond} \\ \text{ to the side lengths of a right triangle.} \end{gathered}`