Question

Compare the function f(x) = 4|x - 1| + 5 and the function g(x) modeled by the graph.What is the difference between the minimum values of f(x) and g(x)?Enter your answer in the box.

Answer 1

• 1Given this function modeled by the graph:

`g(x)`

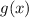
You can identify that its vertex is:

`(-2,1)`

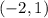
As you can see in the picture below:

Since the function opens upward, its vertex is the minimum point.

Therefore, you can identify that the minimum value of this function is the y-coordinate of the vertex:

`y=1`

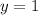
• Given the function:

`f\mleft(x\mright)=4|x-1|+5`

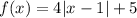
You can identify that it is written in Vertex Form:

`f\mleft(x\mright)=a|x-h|+k`

Where "h" is the x-coordinate of its vertex and "k" is the y-coordinate of the vertex. If:

`a<0`

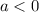
The function opens downward. And if:

`a>0`

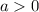
It opens upward.

In this case, you can identify that:

`a=4`

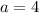
Since it is greater than zero, you can determine that the function opens upward, and therefore, its minimum point is its vertex.

You can also identify that its vertex is:

`(1,5)`

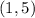
Hence, its minimum value is:

`y=5`

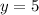
• In order to find the Difference between the minimum values of both functions, you have their minimum values:

`5-1=4`

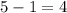
Hence, the answer is:

`4`