Question

Can you please help with 5 I need this done by tonight

Answer 1

Given:

We get the points (5,1), (10, 2), (15,3), and (20, 4) from the table.

Required:

We need to check the relation of the given table.

Step-by-step explanation:

Recall that in a proportional relationship, one variable is always a constant value time the other.

The form of the proportional relationship is

`y=kx`

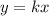
The values x=5 and y=1 can be written as follows.

`1=((1)/(5))\cdot5`

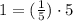
Here we get k=1/5.

The values x=10 and y=2 can be written as follows.

`2=((1)/(5))\cdot10`

Here we get k=1/5.

The values x=15 and y=3 can be written as follows.

`3=((1)/(5))\cdot15`

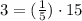
Here we get k=1/5.

The values x=20 and y=4 can be written as follows.

`4=((1)/(5))\cdot20`

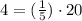
Here we get k=1/5.

There is a common constant k=1/5.

The table represents the proportional relationship.

Final answer:

The table represents the proportional relationship.