Question

write a recursive formula for the given arithmetic sequence, and then find the specified term.a={2,6,10,...}a_1=Answera_n = a_{n-1} + Answera_8 =Answer

Answer 1

Looking at the given arithmetic sequence, we can see that the first term is 2, therefore a1 = 2.

Also, each number is 4 units more than the number before (that is, the common difference of the sequence is 4), so we have the following recursive formula:

`a_n=a_(n-1)+4`

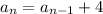
Now, to find the 8th term, let's use the recursive formula until we reach n = 8:

`\begin{gathered} a_4=a_3+4=10+4=14\\ \\ a_5=a_4+4=14+4=18\\ \\ a_6=a_5+4=18+4=22\\ \\ a_7=a_6+4=22+4=26\\ \\ a_8=a_7+4=26+4=30 \end{gathered}`

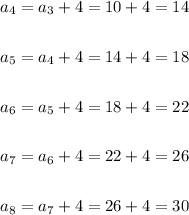
Therefore a8 = 30.