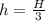Question

A cone with height h is inscribed in a larger cone with height H so that itsvertex is at the centre of the base of the larger cone. Show that the inner conehas a maximum volume when h=1/3H.

Answer 1

Using the diagram:

Step 1: Using similar triangles and simplifying:

`\begin{gathered} (H)/(R)=(H-h)/(r) \\ Making\text{ }h\text{ }subject \\ h=(H)/(R)(R-r) \end{gathered}`

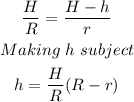
Step 2: Use the Volume of the smaller cone

`\begin{gathered} V(r)=(1)/(3)\pi r^2h \\ Substituting\text{ }h \\ V(r)=(1)/(3)\pi r^2[(H)/(R)(R-r)] \\ V(r)=(\pi H)/(3R)(Rr^2-r^3) \end{gathered}`

Step 3: Differentiating to get maximum value

`\begin{gathered} V^(\prime)(r)=(\pi H)/(3R)r(2R-3r) \\ At\text{ maximum V'\lparen r\rparen=0} \\ r=0\text{ }or\text{ 3r=2R} \\ r=(2R)/(3) \end{gathered}`

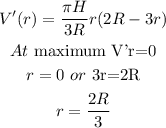
Step 4: Equate radius, r in the height formula from step 1

`\begin{gathered} h=(H)/(R)(R-r) \\ h=(H)/(R)(R-(2R)/(3)) \\ h=(H)/(R)\cdot(R)/(3) \\ h=(H)/(3) \end{gathered}`

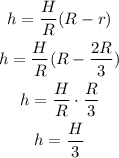
Final answer:

the inner cone has a maximum volume when:

`h=(H)/(3)`