Answer:
Explanation:
The work-energy theorem says that the change in kinetic energy of a system is equal to the work done.

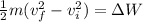
Now in our case
![\begin{gathered} m=1079\operatorname{kg} \\ vf=\text{unknown} \\ v_i=3.00m/s \\ \Delta W=2.00*10^5J \end{gathered}]()
Therefore, the above equation gives

Now we need to solve for v_f .
Mutlipying both sides by 2 gives
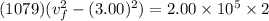
dividing both sides by 1079 gives
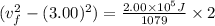
Finally, adding 3.00^2 to both sides gives
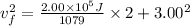
Finally, simplifying the right-hand side gives

taking the square root of both sides gives
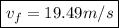
Hence, the final speed of the car is 19.49 m/s.