Answer:
a) Future value = $11,749.38
Interest = $2,844.82
b) Future value = $11,717.79
Interest = $2,813.23
Explanations:
The formula for calculating the future amount (compound amount) is expressed as;
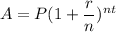
P is the amount invested
r is the rate (in decimal)
n is the compounding time
t is the time (in years)
Given the following parameters:
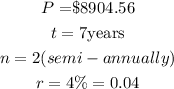
Substitute the given parameters into the formula:

Hence the future value if the amount invested is compounded semiannually is approximately $11,749.38
Calculate the interest;

b) If the amount invested is compounded continuously, this means that
n = 1. Using the previous formula and replacing the value of "n" as 1 will give;

The future value when interest is compounded continuously is approximately $11,717.79
Get the interest if compounded continuously
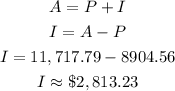
Hence the interest on the amount invested if compounded continuously is $2,813.23