Given the following function
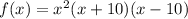
We want to know the maximum number of turning points of this function. To determinate the maximum number of turning points, first we need to understand what is a turning point.
A turning point is is a point where the first derivative is null.
To find the turning points then, we just need to calculate the first derivative and solve for f'(x) = 0.
To find the derivative, we can just expand the polynomial and use the power rule.
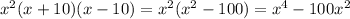

Now, we just need to solve for f'(x) = 0 to find the turning points, but, since we only want to know the maximum amount of turning points is even easier to find. This is a third-degree polynomial, and the solutions for the f'(x) = 0 are the roots of this polynomial. Since it is a third-degree polynomial, the maximum amount of roots is 3.
From the statements of item C, we can see the correct graph is the graph C.