Suppose that EB and DC are parallel; therefore, triangles EAB and DAC are similar triangles due to the AAA postulate. Because those two triangles are similar, the ratio between their corresponding sides is constant; then,
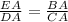
Thus,
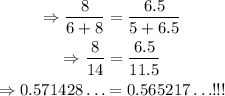
The two quantities are not the same, this is a contradiction. Thus, EB and DC cannot be parallel.