Question

2The high school is hosting an event for seniors but will also allow some juniors toattend. The principal approved the event for 200 students and decided thenumber of juniors should be 25% of the number of seniors. How many juniors willbe allowed to attend?

Answer 1

Given:

The principal approved the event for 200 students.

The number of juniors should be 25% of the number of seniors.

To find:

The number of juniors.

Step-by-step explanation:

Let x be the number of seniors.

According to the problem,

`x+25\%\text{ of }x=200`

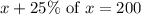
Solve for x we get,

`\begin{gathered} x+(25)/(100)x=200 \\ x+(1)/(4)x=200 \\ (5x)/(4)=200 \\ 5x=800 \\ x=(800)/(5) \\ x=160 \end{gathered}`

So, the number of seniors is 160.

Therefore, the number of juniors must be,

`200-160=40`

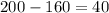
Final answer:

The number of juniors is 40.