Question

Please help me with this problem my son is stuck on this an I need help with getting this answered correctly

Answer 1

Part A.

In this case, we need to find the difference between two consecutive output values. For instance,

`f(-5)-f(-4)=-11-(-3)`

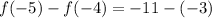
which gives

`f(-5)-f(-4)=-11+3=-8`

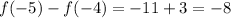
If we choose another pair of consecutive values, we will have the same difference. Then, the answer for part A is -8

Part B.

In this case, we wiil choose any two inputs that are 2 units apart, for instance,

Then, the difference of the outputs is given by

`f(-3)-f(-1)=5-21`

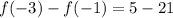
which gives

`f(-3)-f(-1)=-16`

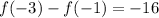
If we choose another pair of consecutive values, we will have the same difference. Then, the answer for part B is: -16

Part C.

Similarly to the previous cases, we need to find the difference between any inputs that are 3 units apart, for instance,

Then, the difference of the outputs is given by

`\begin{gathered} f(-3)-f(0)=5-29 \\ f(-3)-f(0)=-24 \end{gathered}`

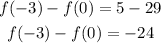
If we choose another pair of consecutive values, we will have the same difference. Then, the answer for part C is: -24

part D.

From the given results, the ratios are;

`\begin{gathered} \text{part A:}\frac{\text{ }f(-5)-f(-4)}{-5-(-4)}=\frac{\text{ }f(-5)-f(-4)}{-1}=(-8)/(-1)=8 \\ \text{part B:}\frac{\text{ }f(-3)-f(-1)}{-3-(-1)}=\frac{\text{ }f(-3)-f(-1)}{-2}=(-16)/(-2)=8 \end{gathered}`

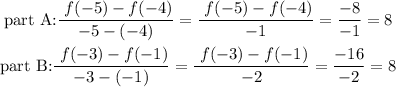
and

`\text{part C:}\frac{\text{ }f(-3)-f(0)}{-3-0}=\frac{\text{-}24}{-3}=8`

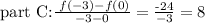
As we can note the ratios are the same and equal to 8.