Question

Which choice is the explicit formula for the following geometric sequence?0.5, -0.1, 0.02, -0.004, 0.0008, ...O A. an = -0.5(0,2)(n-1)B. an = 0.5(0.2)"C. an = 0.5(-0.2)(n-1)D. an = -0.5(0.3)(n-1)E. an = -0.5(-0.2) (n = 1)N

Answer 1

The nth term of a geomeric series having first term 'a' and the common ratio 'r' is given by,

`a_n=a\cdot r^(n-1)`

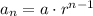
Now, consider the given geometric sequence,

`0.5,-0.1,0.02,-0.004,0.0008,\ldots\ldots`

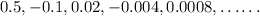
Observe that the first term of the sequence is 0.5,

`a=0.5`

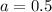
The common difference is calculated as,

`\begin{gathered} r=\frac{a_2}{a_{}} \\ r=(-0.1)/(0.5) \\ r=-0.2 \end{gathered}`

Substitute the values,

`a_n=(0.5)(-0.2)^(n-1)`

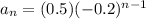
This expression is given in option C. Therefore, option C is the correct choice.