Question

Mary takes a sightseeing tour on a helicopter that can fly 450 miles against a 35 mph headwind. In the same amount of time it can travel 702 miles with a 35 mph tailwind. Find the speed of the helicopter.Provide your answer below:s=____mph

Answer 1

Given:

When flying against a headwind:

Distance = 450 miles

Speed = v - 35 mph

When flying tailwind:

Distance = 702 miles

Speed = v + 35 mph

Let's find the speed of the helicopter.

Apply the formula:

`v=(d)/(t)`

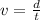
Where:

v is the speed

d is the distance

t is the time

Rewrite the equation for time (t):

`t=(d)/(v)`

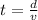
Thus, we have the equations:

Time when flying against headwind:

`t=(450)/(v-35)`

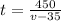
Time when flying tailwind:

`t=(702)/(v+35)`

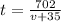
Eliminate the equal sides of the equations and combine.

We have:

`(450)/(v-35)=(702)/(v+35)`

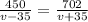
Let's solve for the speed, v.

Cross multiply:

`450(v+35)=702(v-35)`

Apply distributive property:

`\begin{gathered} 450(v)+450(35)=702(v)+702(-35) \\ \\ 450v+15750=702v-24570 \end{gathered}`

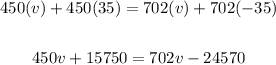
subtract 15750 from both sides:

`\begin{gathered} 450v+15750-15750=702v-24570-15750 \\ \\ 450v=702v-40320 \end{gathered}`

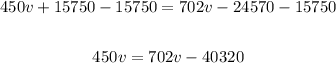
Subtract 702v from both sides:

`\begin{gathered} 450v-702v=702v-702v-40320 \\ \\ -252v=-40320 \end{gathered}`

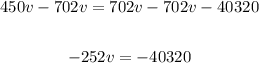
Divide both sides by -252:

`\begin{gathered} (-252v)/(-252)=(-40320)/(-252) \\ \\ v=160 \end{gathered}`

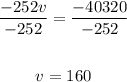
Therefore, the speed of the helicopter is 160 mph

ANSWER:

s = 160 mph