Question

Chandler and Gilbert both currently have a population of 200,000 people. Chandler expects to grow by 2000 people each year. Gilbert expects to grow by 10% each year.a. What is the absolute difference between the population of Chandler compared to Gilbert after 10 years?b. What is the relative difference of the population of Chandler compared to Gilbert after 10 years?

Answer 1

The absolute difference of two real numbers x, y is given by |x - y|. Now we need to know the population of Chandler and Gilbert after 10 years.

Chandler: We have that after ten years the population is 220,000

Gilbert: after ten years the population is

the 1 year after: 200,000 + 20,000 = 220,000

the 2 year after: 220,000 + 22,000 = 242,000

the 3 year after: 242,000 + 24,200 = 266,200

the 4 year after: 266,200 + 26,620 = 292,820

the 5 year after: 292,820 + 29,282 = 322,102

the 6 year after: 322,102 + 32,210.2 = 354,312.2

the 7 year after: 354,312.2 + 35,431.22 = 389,743.42

the 8 year after: 389,743.42 + 38,974.342 = 428,717.762

the 9 year after: 428,717.762 + 42,871.7762 = 471,589.5382

the 10 year after: 471,589.5382 + 47,158.95382 = 518,748.90764

a. So the absolute difference is |518,748.90764 - 220,000 |= 298,748.90764

The relative difference is given bu the formula

`\frac{\lvert{x-y}\rvert}{max{}\lbrace x,y\rbrace}`

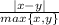
in this case we have that the relative difference is

`\frac{\lvert{518,748.90764-220,000}\rvert}{518,748.90764}=(298,748.90764)/(518,748.90764)`

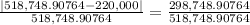
b. 0.57590272