Given:
We get a=6, b=11.9, and c=7, and angle B is 132 degrees.
Required:
We need to classify the given triangle.
Step-by-step explanation:
Consider the cosine law.
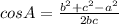
Substitute a=6, b=11.9, and c=7 in the formula.
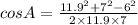
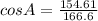
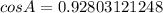
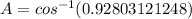
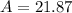
Recall that an obtuse angle is an angle greater than 90°.
The given triangle has an obtuse angle at B.
The given triangle is Obtuse.
Recall that an isosceles triangle is a triangle with (at least) two equal sides.
The given triangle has three different sides.
The given triangle is not an isosceles triangle.
Recall that a scalene triangle is a triangle in which all three sides are in different lengths, and all three angles are of different measures.
The given triangle is a scalene triangle.
Recall that an acute-angled triangle is a type of triangle in which all the three internal angles of the triangle are acute,
There is an obtuse angle.
The given triangle is not an acute triangle.
Recall that a right-angled triangle is a triangle, that has one of its interior angles equal to 90 degrees.
There is no 90 degrees angle.
The given triangle is not a right-angled triangle.
Recall that an equilateral triangle is a triangle with all three sides of equal length.
The given triangle is not an equilateral triangle since there are all three sides of different lengths.
Final answer:
Obtuse, Scalene