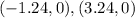ANSWER
Step-by-step explanation
We want to find the x intercepts of the parabola with vertex (1, 20) and y intercept (0, 16).
To do this, first find the equation of the parabola.
The vertex form of the equation of a parabola is:
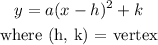
Therefore, we have:
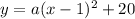
To find the value of a, substitute the values of x and y of the y intercept into the equation:
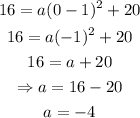
Therefore, the equation of the parabola in vertex form is:
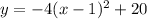
Now, write it in standard form:
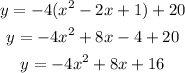
To find the x intercepts, find the values of x when y = 0:
![\begin{gathered} -4x^2+8x+16=0 \\ \text{Solve using Quadratic formula:} \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ a=-4;b=8;c=16 \\ x=\frac{-8\pm\sqrt[]{8^2-4(-4)(16)}}{2(-4)}=\frac{-8\pm\sqrt[]{64+256}}{-8} \\ x=\frac{-8+\sqrt[]{320}}{-8};x=\frac{-8-\sqrt[]{320}}{-8} \\ \Rightarrow x=(-8+17.89)/(-8);x=(-8-17.89)/(-8) \\ x=-1.24;x=3.24 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/98eqfpsyrso4soy6p73crbi2kgm95na4f3.png)
Therefore, the x intercepts are: