Question

Find the Margin of error and 95% of confidence interval for the survey result described.according to a poll of 705 people, about one third (34%) of Americans keep a dog for protection

Answer 1

We have that the poll had 705 participants, and one third keeps a dog for protection. We can write this information with the following variables:

`\begin{gathered} n=705 \\ \text{Number of people that keeps a dog for protection:} \\ (705)/(3)=235 \\ \Rightarrow p=(235)/(705) \end{gathered}`

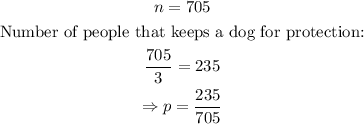
since we want the 95% of confidence, we have to use the following z score:

`z_(95\%)=1.96`

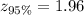
then, we can find the margin of error with the following equation:

`m=z_(\alpha)\cdot\sqrt[]{(p(1-p))/(n)}`

in this case, we have the following:

`m=1.96(\sqrt[]{(((235)/(705))(1-(235)/(705)))/(705)})=1.96(0.018)=0.04=4\%`

therefore, the margin of error is 4% and the confidence interval is:

`\begin{gathered} (p-m,p+m) \\ \Rightarrow((235)/(705)-0.04,(235)/(705)+0.04)=(0.293,\text{0}.373) \end{gathered}`

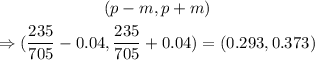
therefore, the proportion of americans that keep a dog for protection is between 29.3% and 37.3%