Question

11) The county fair is a popular field trip destination. This year the senior class at High School A andthe senior class at High School B both planned trips there. The senior class at High School Arented and filled 3 vans and 8 buses with 322 students. High School B rented and filled 8 vansand 6 buses with 322 students. Every van had the same number of students in it as did the buses.Find the number of students in each van and in each bus.

Answer 1

We are given that high school A filled 3 vans and 8 buses with 322 students. Let "x" be the number of students in a van and "y" the number of students in the bus then this can be written mathematically as:

`3x+8y=322,(1)`

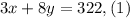
High school B filled 8 vans and 6 buses with 322. Since each van and bus has the same number of students then we can write this as:

`8x+6y=322,(2)`

We get 2 equations and 2 variables. To determine the solution we will solve for "x" in equation (1). To do that we will subtract "8y" from both sides:

`3x=322-8y`

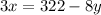
Now, we divide both sides by 3:

`x=(322-8y)/(3)`

Now, we substitute the value of "x" in equation (2):

`8((322-8y)/(3))+6y=322`

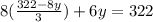
Now, we apply the distributive law on the parenthesis:

`(2576-64y)/(3)+6y=322`

Now, we multiply both sides by 3:

`2576-64y+18y=966`

Now, we add like terms:

`2576-46y=966`

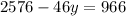
Now, we subtract 2576 from both sides:

`\begin{gathered} -46y=966-2576 \\ -46y=-1610 \end{gathered}`

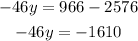
Now, we divide both sides by -46:

`y=-(1610)/(-46)=35`

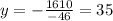
Now, we substitute the value of "y" in equation (1):

`3x+8(35)=322`

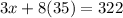
Solving the product:

`3x+280=322`

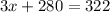
Now, we subtract 280:

`\begin{gathered} 3x=322-280 \\ 3x=42 \end{gathered}`

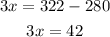
Dividing by 3:

`x=(42)/(3)=14`

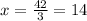
Therefore, there are 14 students in the van and 35 in the bus.