1 Answer

Baseten · Answer 1 · 2023-01-15T15:16:37+0000

To find the solution of the equation (x), follow the steps below.

Step 01: Add 8 to both sides of the equation.

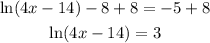
$\begin{gathered} \ln (4x-14)-8+8=-5+8 \\ \ln (4x-14)=3 \end{gathered}$

Step 02: Use the base for both sides.

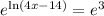
$e^(\ln (4x-14))=e^3$

Step 03: Solve e^ln=1

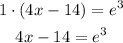
$\begin{gathered} 1\cdot(4x-14)=e^3 \\ 4x-14=e^3 \end{gathered}$

Step 04: Add 14 to both sides, then divide the sides by 4.

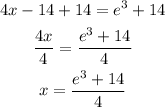
$\begin{gathered} 4x-14+14=e^3+14 \\ (4x)/(4)=(e^3+14)/(4) \\ x=(e^3+14)/(4) \end{gathered}$

Done! You found the exact solution.

Step 05: To find the aproximate solution, use the value of e.

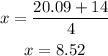
$\begin{gathered} x=(20.09+14)/(4) \\ x=8.52 \end{gathered}$

Answer: x = 8.52.

Please log in or register to add a comment.