Question

The volumes of two similar figures are given. The surface area of the smaller figure is given. Find the surface area of the larger figure. VA = 27m3 and VB = 64m3 and SA = 63m2

Answer 1

,For similar figures we have:

`\begin{gathered} (q)^3=(V_b)/(V_a) \\ (q)^2=(S_b)/(S_a) \end{gathered}`

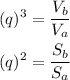
where q stands for the scale factor, V for the volume and S for the area.

Now, because we have both volumes, we calculate q as follows:

`\begin{gathered} q^3=(64)/(27) \\ q=\sqrt[3]{(64)/(27)} \\ q=(4)/(3) \end{gathered}`

Now, we use the value found for q and the given value of Sa to find the value of Sb, as follows:

`\begin{gathered} ((4)/(3))^2=(S_b)/(63) \\ S_b=(63\cdot16)/(9) \\ \\ S_b=112m^(2) \end{gathered}`

From the solution developed above, we are able to conclude that the solution is Sb = 112 m²