Given the word problem, we can deduce the following information:
1. The two planes are 3950 miles apart.
2. Their speeds differ by 40 mph.
3. Time =5 hours
To determine the speed of each plane, we first let:
x= speed of the fist plane
x+40 =speed of the second plane
Based on the above information, the combined speed is 2x+40. Our equation would be:
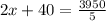
Next, we find the value of x:

Hence,
x= speed of the fist plane=375 mph
x+40 =speed of the second plane=375+40= 415 mph