Given:
Number of hours, t = 14 hours
Distance = 52 miles
Speed travelling = 8 mph
Let's find the speed of the current.
Apply the formula:

Here, we have the system of equations:
For time travelling up: 14 = 52/8-c
For time travelling down: 14 = 52/8 + c
Where c is the speed of the current.
Hence, we have:
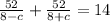
Let's solve the equation for c.
Multiply all terms by (8-c)(8+c):
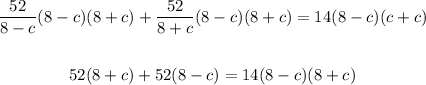
Solving further, expand using FOIL method and apply distributive property:
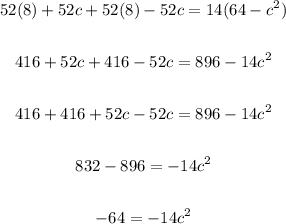
Solving further:
Divide both sides by -14

Therefore, the speed of the current was 2.14 miles per hour.
ANSWER:
2.14 mph