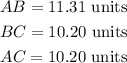Answer:
The length of the line AB, BC, and, AC are;
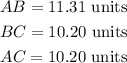
Step-by-step explanation:
We want to find the length of the line AB, BC, and, AC.
Applying the formula for calculating the distance between two points;
![d=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/nkjymhkzx142t3t66rnvx6qo7qj0ya3b8k.png)
We are given the coordinates of each point as;
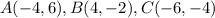
So, the length AB is;
![\begin{gathered} AB=\sqrt[]{(-2_{}-6_{})^2+(4_{}-(-4))^2} \\ AB=\sqrt[]{(-8)^2+(8)^2} \\ AB=\sqrt[]{64^{}+64} \\ AB=\sqrt[]{128} \\ AB=11.31\text{ units} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/m8gz1lx4tv0zhc2clv4kle8gaa1228iox1.png)
Length BC is;
![\begin{gathered} BC=\sqrt[]{(-4_{}-(-2)_{})^2+(-6-4)^2} \\ BC=\sqrt[]{(-4_{}+2_{})^2+(-10)^2} \\ BC=\sqrt[]{(-2_{})^2+(-10)^2} \\ BC=\sqrt[]{4+100} \\ BC=\sqrt[]{104} \\ BC=10.20\text{ units} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/fyl7j5jwityfkvbtrzvo6jvxvcjcwgvt3n.png)
Length AC is;
![\begin{gathered} AC=\sqrt[]{(-4_{}-6_{})^2+(-6-(-4))^2} \\ AC=\sqrt[]{(-10))^2+(-6+4)^2} \\ AC=\sqrt[]{(-10)^2+(-2)^2} \\ AC=\sqrt[]{100+4} \\ AC=\sqrt[]{104} \\ AC=10.20\text{ units} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/gdoeqyl3dh1uavnnq0vyrsg0deuu7yutjz.png)
Therefore, the length of the line AB, BC, and, AC are;