We need to multiply each equation by different factors so that the coefficients next to the x-variable in each new equation are opposite numbers.
Multiplying the first equation by -4, we get:
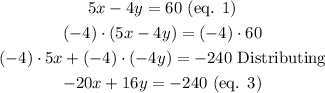
Multiplying the second equation by 5, we get:
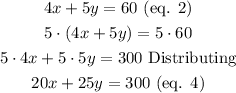
And now, the coefficients of the x-variable of equations 3 and 4 are -20 and 20.