We will have the following:
First, we find all the forces in x & y, that is:
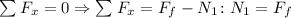
Here Ff is the frictional force and N1 the normal force on the point where the ladder is resting.
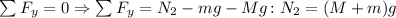
Here N2 is the normal force of the resting point of the ladder on the ground. M is the mass of the person and m is the mass of the ladder.
Then we make sure that the ladder won't rotate, that is the momentum will be 0, that is:
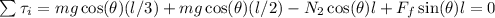
Here "l/3" represents the positons of the person to climb, and "l/2" represents the position of the center of mass of the ladder.
Then, we remember that we are given the static friction coefficient, and replace:
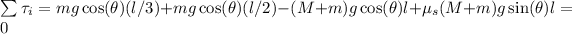
Then we divide the whole expression by cos(theta) in order to eliminate all extra trigonometric values and determie the angle:
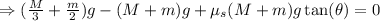
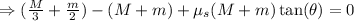
![\Rightarrow\tan (\theta)=((M+m)-((M)/(3)+(m)/(2)))/((M+m)\mu_s)\Rightarrow\tan (\theta)=\frac{(60\operatorname{kg}+10\operatorname{kg})-(\frac{60\operatorname{kg}}{3}+\frac{10\operatorname{kg}}{2})}{(60\operatorname{kg}+10\operatorname{kg})(0.50)}]()
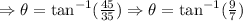
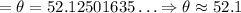
So, the angle would be approximately 52.1°.
***Screenshot***