Let the price of a bike at Store B be k
The price of a bike at Store A is 5/6 of the price at store B, which means
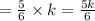
If the price of a bike at Store A is $150.60, i.e
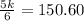
Solve to find k, i.e the price of a bike at Store B
Crossmultiply
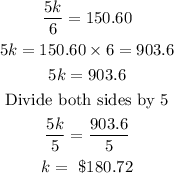
The price of a bike at store B is k = $180.72
The amount saved if the bike is bought at Store A is
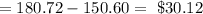
Hence, the amount saved by buying the bike at Store A is $30.12