1 Answer

Ask a Question

Eze · Answer 1 · 2023-07-08T05:57:53+0000

To answer this question, we can proceed as follows:

As we can see from the above figure, the triangles PQR and MQN are similar triangles. If they are similar, then their corresponding sides are in proportion. Then, we have:

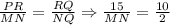
$(PR)/(MN)=(RQ)/(NQ)\Rightarrow(15)/(MN)=(10)/(2)$

Then, we need to solve the equation for MN, then we have:

$(15)/(MN)=5\Rightarrow(MN)/(15)=(1)/(5)\Rightarrow MN=(15)/(5)\Rightarrow MN=3\operatorname{cm}$

Therefore, the value for the side MN is 3 cm (option b).

In A PQR, point Mis on PQ, and point N is on QR, so that MN ||PR. It is given that-example-1

In A PQR, point Mis on PQ, and point N is on QR, so that MN ||PR. It is given that-example-2

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions