Question

at skiing competition , a 55 kg skier is coasting down a 25° slope as shown in figure. near the top of the slope his speed is 3.8 m/s . the coefficient of friction between the ski boots and the surface of the slope is 0.14 . by using the work energy theorem , determine the skier's speed after he moved 57 m downhill

Answer 1

Given data:

* The mass of the skier is m = 55 kg.

* The angle of the slope is,

`\theta=25^(\circ)`

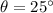
* The initial velocity of the skier at the top is,

`u=3.8\text{ m/s}`

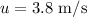
* The coefficient of friction between the ski boot and slope is,

`\mu=0.14`

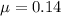
* The distance traveled by the skier along the inclined plane is,

`S=57\text{ m}`

Solution:

The diagrammatic representation of the given case is,

The angle of the inclined plane with the vertical axis is,

`\begin{gathered} \alpha=180^(\circ)-90^(\circ)-\theta \\ \alpha=90^(\circ)-\theta \end{gathered}`

Thus, the component of the weight of skier along the inclined plane is,

`\begin{gathered} F_1=mg\cos (90^(\circ)-\theta)_{} \\ F_1=mg\sin (\theta) \end{gathered}`

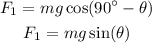
where g is the acceleration due to gravity,

Substituting the known values,

`\begin{gathered} F_1=55*9.8*\sin (25^(\circ)) \\ F_1=227.79\text{ N} \end{gathered}`

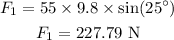
The component of weight perpendicular to the inclined plane is,

`\begin{gathered} F_2=mg\sin (90^(\circ)-\theta) \\ F_2=mg\cos (\theta) \end{gathered}`

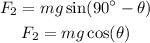
Substituting the known values,

`\begin{gathered} F_2=55*9.8*\cos (25^(\circ)) \\ F_2=488.5\text{ N} \end{gathered}`

From the diagram, the normal force acting on the skier is,

`\begin{gathered} F_N=F_2 \\ F_N=488.5\text{ N} \end{gathered}`

The frictional force acting on the skier in terms of the normal force is,

`\begin{gathered} F_r=\mu F_N \\ F_r=0.14*488.5 \\ F_r=68.39\text{ N} \end{gathered}`

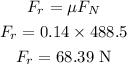
Thus, the net force acting on the skier down the inclined plane is,

`\begin{gathered} F=F_1-F_r_{} \\ F=227.79-68.39 \\ F=159.4\text{ N} \end{gathered}`

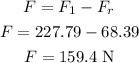
According to Newton's second law, the acceleration of the skier is,

`\begin{gathered} F=ma \\ a=(F)/(m) \\ a=(159.4)/(55) \\ a=2.9ms^(-2) \end{gathered}`

By the kinematics equation, the speed of the skier after moving to distance S is,

`\begin{gathered} v^2-u^2=2aS \\ v^2-3.8^2=2*2.9*57 \\ v^2-14.44=330.6 \\ v^2=330.6+14.44 \end{gathered}`

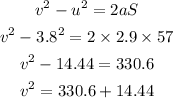
By simplifying,

`\begin{gathered} v^2=345.04 \\ v=18.6\text{ m/s} \end{gathered}`

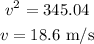
Thus, the speed of the skier after moving 57 m downhill is 18.6 meters per second.