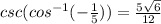Recall that the tangent function is the ratio of the opposite side of the angle and the adjacent side of the angle.
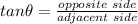
The function in letter "a" can be written as:
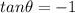
Therefore, we can say that:

From this, we can conclude that the opposite side and the adjacent side both have a length of 1 unit in order to have that ratio of -1. See the illustration below:
Based on the properties of one of the special right triangles whose sides are in the ratio 1:1:√2 just like the triangle above, the measure of each angle is 45°-45°-90°.
Therefore, the measure of the angle is 45°. Since the value of tan θ is negative, then the exact value of the expression tan^-1 (-1) is -45°.
Let's solve part b.
Recall that the cosine function is the ratio of the adjacent side and the hypotenuse of a right triangle.
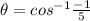
Hence, we can conclude that the adjacent side measures 1 unit while the hypotenuse measures 5 units.
Let's also recall that the cosecant function is the ratio of the hypotenuse and the opposite side of the triangle. Since we already have the length of the hypotenuse, let's solve for the opposite side using the Pythagorean Theorem.
Applying the Pythagorean Theorem, the length of the opposite side is:
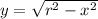
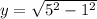
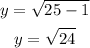
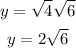
The length of the opposite side is 2√6.
Now that we have the length of the opposite side, let's now find the value of csc θ.
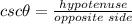

Rationalize the denominator by multiplying both numerator and denominator by 2√6.
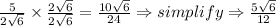
Therefore, the exact value of csc θ or csc (cos^-1 (-1/5)) is (5√6)/12.