Question

Use the formula for present value of money to calculate the amount you need to invest now in onelump sum in order to have $100,000 after 18 years with an APR of 11% compounded quarterly.Round your answer to the nearest cent, if necessary.

Answer 1

In order to determine the money you have to invest now to obtain $100,000 after 18 years, use the following formula:

`A=P(1+(r)/(n))^(nt)`

where,

P: principal = ?

A: amount after t years = 100,000

r: APR in decimal form = 0.11 (11%)

n: times of the compounded interest at year = 4 (quarterly)

t: time = 18 (years)

Solve the equation above for P, replace the values of the other parameters and simplify:

`\begin{gathered} 100000=P(1+(0.11)/(4))^(4*18) \\ 100000=P(1.0275)^(72) \\ P=(100000)/((1.0275)^(72)) \\ P\approx14181.04 \end{gathered}`

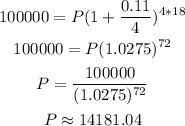
Hence, you need to invest approimately $14,181.04 to obtain $100,000 after 18 years.