Question

Find the annual rate of interest.Principal = 7800 rupeesPeriod = 7 yearsTotal amount = 11349 rupeesAnnual rate of interest =

Answer 1

The future value for simple interest is given by the following formula:

`A=P(1+rt)`

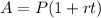
Where A is the future value, r is the rate of interest, t the time and P the present value. Now we solve for the rate of interest "r" first by dividing both sides by "P":

`(A)/(P)=1+rt`

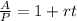
Now we subtract 1 to both sides:

`(A)/(P)-1=rt`

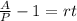
Dividing both sides by "t":

`(A)/(Pt)-(1)/(t)=r`

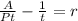
Replacing the known values:

`(11349)/((7800)(7))+(1)/(7)=r`

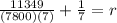
Solving the operations:

`0.35=r`

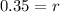
Therefore, the annual rate of interest is 35%.