Given:
Two planes leave from Atlanta, Georgia.
One makes a 7.4 hours flight to Seattle, Washington and the other makes a 2.6 hours flight to Boston, Massachusetts.
The plane to Boston averages 60 mph slower than the plane to Seattle.
The total distance traveled by both plan is 3125 mi.
Required:
We need to find the Average speed of each plane
Step-by-step explanation:
Speed of Seattle plane is S
Speed of Boston plane is B
by The plane to Boston averages 60 mph slower than the plane to Seattle
we can say that
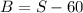
Formula of distance is the rate of speed times time
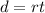
Where d is distance
r is rate of speed
t it time
Now total distance traveled by both plane is 3124 mi
so
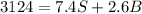
substitute the value of B
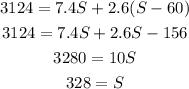
Now to find B
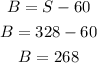
Final answer:
Average speed of S is 328 mph
Average speed of B is 268 mph