Question

3s +13 - t6r-35-AS-)+27 -38-12-17 4r +5946tR+26-5-bre 4+25+8 -1806) - 39:- 525-948-44 Er+15-12-11 - 3 - 11) 5x - 4y + 2z = 21 - 35 +13 +224) $24 -x - 5y +62=-24 x - 4y +52=-21 --+13-11. 12, 6 Sr 37

Answer 1

Given data:

The first equation is 5x-4y+2z=21.

The second equation is -x-5y+6z= -24.

The third equation is -x-4y+5z=-21.

Multiply 5 by second equation and add first and second equation.

`\begin{gathered} 5(-x-5y+6z)+5x-4y+2z=5(-24)+21 \\ -29y+32z=-99\ldots\ldots\ldots\ldots\ldots\text{......}(A) \end{gathered}`

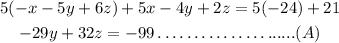
Multiply 5 by third equation and add first and second equation.

`\begin{gathered} 5(-x-4y+5z)+5x-4y+2z=5(-21)+21 \\ -24y+27z=-84 \\ -8y+9z=-28 \\ z=(8y-28)/(9) \end{gathered}`

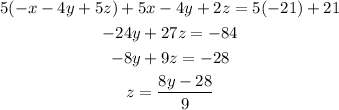
Substitute the above value of z in equation(A).

`\begin{gathered} -29y+32\frac{(8y-28_{})}{9}=-99 \\ -261y+256y--896=-891 \\ -5y=5 \\ y=-1 \end{gathered}`

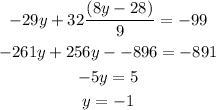
The value of z is,

`\begin{gathered} z=(8(-1)-28)/(9) \\ =-4 \end{gathered}`

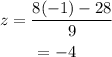
The value of x is,

`\begin{gathered} 5x-4(-1)+2(-4)=21 \\ 5x=25 \\ x=5 \end{gathered}`

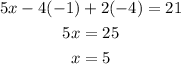
Thus, the value of x is 5, the value of y is -1, and the value of z is -4.