Answer:
x = 25 and x = 5
Step-by-step explanation:
Step 1
b is the number beside the x, so (b/2)^2 is equal to:
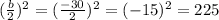
So, if we add 225 to both sides of the equation, we get:
x² - 30x = -125
x² - 30x + 225 = -125 + 225
x² - 30x + 225 = 100
Step 2
Now, we can factor the left side of the equation, the expression x² - 30x + 225 is a perfect square trinomial because the first and third terms are perfect squares and the second term is 2 times the square root of the other terms
![\begin{gathered} \sqrt[]{x^2}=x \\ \sqrt[]{225}=15 \\ -30x=-2(15)(x) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/bc9hdqsmozr7jt9ent4u3gi5mqfza7ia3h.png)
Therefore, the factorization will be:
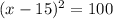
Step 3
Then, the square root of both sides is equal to:
![\begin{gathered} \sqrt[]{(x-15)^2}=\sqrt[]{100} \\ x-15=10_{} \\ or \\ x-15=-10 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9rnxn9iajvqmky480dxrwwutp5lsn0m9vy.png)
Step 4
Therefore, the solutions of the equation are:
x - 15 = 10
x - 15 + 15 = 10 + 15
x = 25
or
x - 15 = -10
x - 15 + 15 = -10 + 15
x = 5
Therefore, the solution of the equation are:
x = 25 and x = 5