Question

Solve the equation by completing the square. Show your work. X^2 - 30x = -125Step 1: Add (b/2)^2 to both sides of the equation.Step 2: Factor the left side of the equation. Show your work.Hint: It is a perfect square trinomial.Step 3: Take the square root of both sides of the equation from Step 2. Step 4: Simplify the radical and solve for x. Show your work.

Answer 1

x = 25 and x = 5

Step-by-step explanation:

Step 1

b is the number beside the x, so (b/2)^2 is equal to:

`((b)/(2))^2=((-30)/(2))^2=(-15)^2=225`

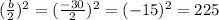
So, if we add 225 to both sides of the equation, we get:

x² - 30x = -125

x² - 30x + 225 = -125 + 225

x² - 30x + 225 = 100

Step 2

Now, we can factor the left side of the equation, the expression x² - 30x + 225 is a perfect square trinomial because the first and third terms are perfect squares and the second term is 2 times the square root of the other terms

`\begin{gathered} \sqrt[]{x^2}=x \\ \sqrt[]{225}=15 \\ -30x=-2(15)(x) \end{gathered}`

Therefore, the factorization will be:

`(x-15)^2=100`

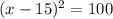
Step 3

Then, the square root of both sides is equal to:

`\begin{gathered} \sqrt[]{(x-15)^2}=\sqrt[]{100} \\ x-15=10_{} \\ or \\ x-15=-10 \end{gathered}`

Step 4

Therefore, the solutions of the equation are:

x - 15 = 10

x - 15 + 15 = 10 + 15

x = 25

or

x - 15 = -10

x - 15 + 15 = -10 + 15

x = 5

Therefore, the solution of the equation are:

x = 25 and x = 5