Step 1: State the given coordinates in the question
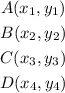
Step 2: Find the slope of Line segment AB
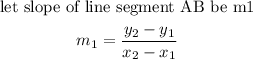
Step 3: Find the slope of the line segment CD
Step 4: State the condition for which line AB and line CD are perpendicular to each other
The condition for which two lines are perpendicular to each other is that the slope of one of the lines is equal to the negative inverse of the other line. This can be represented mathematically by applying it the line AB and line CD
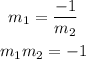
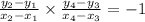
Hence, the correct option is OPTION C