Lateral Surface Area and Volume of a Cone
Given a cone of radius r and height h, the lateral surface area can be calculated as follows:
![A_l=\pi r\sqrt[]{r^2+h^2}](https://img.qammunity.org/2023/formulas/mathematics/college/q7p2jzp8mwe8of5rqn28a6a1mxaal8kutu.png)
And the volume is:
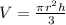
The image shows a cone and we are given the diameter of the base and the height.
We need first to calculate the radius of the base:
![\begin{gathered} r=(d)/(2) \\ r=\frac{11.4\operatorname{cm}}{2} \\ r=5.7\operatorname{cm} \end{gathered}]()
Now calculate the lateral surface area:
![A_l=\pi\cdot5.7cm\cdot\sqrt[]{(5.7cm)^2+(16.2\operatorname{cm})^2}]()
Calculating:
![A_l=17.907cm\cdot\sqrt[]{32.49cm^2+262.44\operatorname{cm}^2}]()
![\begin{gathered} A_l=17.907cm\cdot\sqrt[]{294.93\operatorname{cm}} \\ A_l=17.907cm\cdot17.17\operatorname{cm} \\ A_l=308\operatorname{cm} \end{gathered}]()
Rounding to the nearest whole number, the area is 308 square cm
Now for the volume:
![V=\frac{\pi(5.7cm)^2(16.2\operatorname{cm})}{3}]()
Calculating:
![\begin{gathered} V=(1653.5396)/(3) \\ V=551\operatorname{cm}^3 \end{gathered}]()
Rounding to the nearest whole number, the volume is 551 cubic cm