Let x be the amount invested in the 6% account and y be the amount invested in the 10%. then we can set the following system of equations:
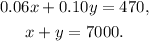
Substracting y from the second equation we get:
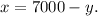
Substituting the above equation in the first one we get:
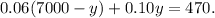
Simplifying the above result we get:
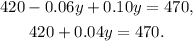
Subtracting 420 from the above equation we get:
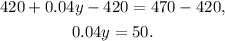
Dividing the above equation by 0.04 we get:
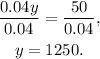
Finally, substituting y=1250 at x=7000-y we get:
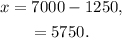
Answer:
$5750 at 6%.
$1250 at 10%.