Question

15. The average battery life of 2800 manufactured cell phones is recordedand normally distributed. The mean battery life is 12 hours with astandard deviation of 1.0 hours. Find the number of phones whohave a battery life in the 13 to 14 range.*

Answer 1

Data given;

`\begin{gathered} \mu=12hrs \\ \sigma=1hr \\ x=13\text{ and 14} \\ Z=\text{?} \end{gathered}`

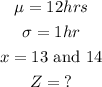
We have to find the Z score within both ranges, we use the formula below, substituting the given values.

`\begin{gathered} Z=(x-\mu)/(\sigma) \\ Z_(13)=(13-12)/(1)=(1)/(1)=1 \\ Z_(14)=(14-12)/(1)=(2)/(1)=2 \end{gathered}`

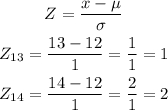
Since the Z-scores are known, we will get the probability from the Z-score table using the range (1

From the Z-score table, P(1

The number of phones that will have battery life in the 13 to 14 hours range will be;

0.13591 x 2800 = 380.548

Therefore, the number of phones that will have battery life in the 13 to 14 hours range is approximately 381 phones to the nearest whole number since a phone is whole and can not be a fraction.