The sum of the first nth terms of a geometric sequence is given by:
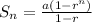
where a is the first term and r is the common ratio.
We know the geometric series is given by:
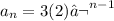
which means that the first term is 3 and the common ratio is 2. Since we want to know the sum of the first nth terms this means that n=10; plugging these values in the expression for the sum we have:
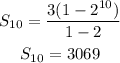
Therefore, the sum we are looking for is 3069