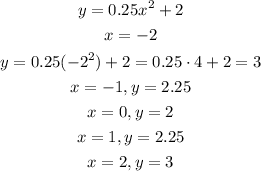This is a paraola: y = 1 is the directrix (it is perpendicular to the axis of symmetry); the focus is (0, 3)
The vertex of the parabola (which must also be on the parabola) is at (0, 1) because it is at a distance of 1 away; it is the nearest point to the point y = 1 & is at a distance 1 away from (0, 3)
The distance of the point (x,y) from the point (0,3) is gotten by using the formula for distance between two points (Pythagoras theorem):
![\begin{gathered} \sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}\Rightarrow\sqrt[]{(x-0)^2+(y-3)^2} \\ \text{the distance from y=1 is given by y-1} \\ (y-1)^2=x^2+(y-3)^2 \\ x^2=(y-1)^2-(y-3)^2 \\ x^2=\lbrack y(y-1)-1(y-1)\rbrack-\lbrack y(y-3)-3(y-3)\rbrack \\ x^2=y^2-y-y+1-(y^2-3y-3y+9) \\ x^2=y^2-y^2-2y-(-6y)+1-9 \\ x^2=4y-8 \\ 4y=x^2+8\Rightarrow y=(1)/(4)x^2+2 \\ y=(1)/(4)x^2+2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/zxq80or8b5btt4lab257r9piq42ifwabgf.png)