Given:
Confidence level = 98%
Margin of error, E = 2% = 0.02
Let's find the number of students the instructor should sample.
Here, we are to find the sample size (n).
We have:

At 98% confidence level, we have:


Using the z-score table, we have:
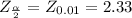
To find the sample size(number of students) n, we have:

Thus, we have:
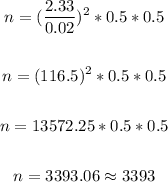
Therefore, the statistics instructor should sample 3393 students.
ANSWER:
3393