Considering the form:

where y is the variable that depends on x, m changes depending on the value of x, and b is constant.
Then, in our problem:
• y ,is the cost of the chauffeured car service for both equations.
,
• x ,is the miles traveled.
,
• m ,is 4 in the first and 2 in the second.
,
• b ,is 3 in the first and 19 in the second.
Then, replacing the latter we can build our equations.
• Equation 1 ,(first service)
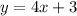
• Equation 2 ,(second service)
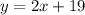
Solving the system of equations by substitution.
0. Replacing ,Equation 2 ,in equation ,1,:
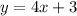

2. Grouping similar terms and solving for x
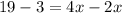
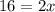
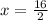
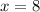
3. Replacing this value in Equation 2 to get y:

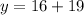
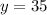
Answer: at 5 miles the two companies charge the same total fare of $35.