Let's draw an illustration of the Triangle ABC, the midpoint of BC which is Point D, and the line AD as the median of triangle ABC.
First, let us solve how we got the coordinates of Point D at (-4, 4).
Since D is the midpoint of BC, then we added the x coordinates of B and C, then divide the result by 2. We also added the y coordinates of B and C, then divide the result by 2.
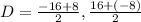
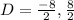
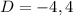
Hence, point D is located at (-4, 4).
Now, to determine the equation the median shown by line AD, we use the two-point form formula.
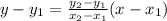
For our (x₁, y₁), we will use point A at (-5, 1). In this case, x₁ = -5 and y₁ = 1.
For our (x₂, y₂), we will use point D at (-4, 4). In this case, x₂ = -4 and y₂ = 4.
Let's plug them into the formula above and solve.
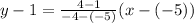
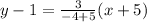
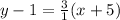
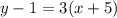
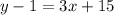
Subtract y and 15 on both sides of the equation.
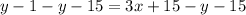
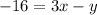
Hence, the equation of the median is -16 = 3x - y or 3x - y = -16 (Option C).